
程序员考试考点分析与真题详解:斐波纳契数列
希赛网 2023-04-14 16:05:58
1.6.1 斐波纳契数列
问题描述:编写计算斐波纳契(Fibonacci)数列,数列大小为n。
无穷数列1.1.2.3.5.8.13.21.35.…称为斐波纳契数列,其递归定义如下:
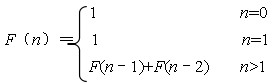
由斐波纳契数列的递归定义可知,当n大于1时,这个数列第n项的数值是它前面两项之和。由于递归算法的执行过程分递推和回归两个阶段,在递推阶段,程序把较复杂的问题(规模为n)的求解推到比原问题简单一些的问题(规模小于n)的求解,在回归阶段,程序由在规模很小时求得的解得到较复杂问题的解。因此,对于斐波纳契数列的求解,要得到数列第n项的值,就必须求得数列第n–1项的值。同理,要求得数列第n–1项的值,就必须求得数列第n–2项的值,依次递推下去,最后需要求得数列第1项和第0项的值,递推部分结束。又当n等于0和1时,其数值为1.根据这些值可求出数列第2项的值,再根据数列第2项的值可得到第3项的值,依次回归,最后可依次得到数列第n–2、n–1和n项的值。由这个例子,我们可以很清楚地了解递归的形式和过程。该问题程序实现如下:
【程序1-2】
# include< stdio.h >
int F(int n)
{if(n==0)return 1;
if(n==1)return 1;
if(n>1)return F(n-1)+F(n-2); /*递归*/
}
main(){
int i,n,m;
printf("please input n: \n");
scanf("%d",&n);
printf("the Fibonacci is : ");
for(i=0;i<=n;i++){
m=F(i);
printf("%d,",m);
}
}








