
程序员考试考点分析:二叉排序树
什么是二叉排序树,又称为二叉查找树,其定义为:二叉排序树或者是一棵空树,或者是具有如下性质(BST性质)的二叉树。
(1)若它的左子树非空,则左子树上所有结点的值均小于根结点;
(2)若它的右子树非空,则右子树上所有结点的值均大于根结点;
(3)左、右子树本身又各是一棵二叉排序树。
例如,图1-8就是一棵二叉排序树。
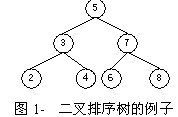
根据二叉排序树的定义可知,如果中序遍历二叉排序树,就能得到一个排好序的结点序列。二叉排序树上有查找、插入和删除3种操作。下面,我们假设二叉排序树的结点只存储结点的键值,其类型与前面的二叉树的结点类型相同。
1.静态查找
静态查找是在二叉排序树上查找键值为key的结点是否存在,可按以下步骤在二叉排序树ST上找值为key的结点:
(1)如果二叉排序树ST为空二叉树,则查找失败,结束查找;
(2)如果二叉排序树根结点的键值等于key,则查找成功,结束查找;
(3)如果key小于根结点的键值,则沿着根结点的左子树查找,即根结点的左子树作为新的二叉排序树ST继续查找;
(4)如果key大于根结点的键值,则沿着根结点的右子树查找,即将根结点的右子树作为新的二叉排序树ST继续查找。
2.动态查找
在二叉排序树上,为插入和删除操作而使用的查找称为动态查找,动态查找应得到两个指针,一个指向键值为key的结点,另一个指向该结点的父结点。为此,查找函数可设4个参数:查找树的根结点指针root、待查找值key、存储键值为key结点的父结点的指针pre,存储键值为key以及结点的指针p.但函数要考虑以下几种不同的情况:
(1)二叉排序树为空,查找失败,函数使*p=NULL,*pre=NULL;
(2)二叉排序树中没有键值为key的结点,函数一直寻找至查找路径的最后一个结点,*pre指向该结点,*p=NULL,如果插入键值为key的结点,就插在该结点下;
(3)查找成功,*p指向键值为key的结点,*per指向它的父结点。
3.插入结点
首先利用动态查找函数确定新结点的插入位置,然后分以下几种情况作为相应的处理:
(1)如果相同键值的结点已在二叉排序中,则不再插入;
(2)如果二叉排序为空树,则以新结点为二叉排序树;
(3)根据要插入结点的键值与插入后的父结点的键值比较,就能确定新结点是父结点的左子结点,还是右子结点,并进行相应的插入。
4.删除结点
删除二叉排序树上键值为key的结点的操作可按以下步骤进行。
(1)调用查找函数确定被删结点的位置;
(2)如果被删除结点不在二叉排序树上,则函数返回。否则,按以下情况分别处理。
①如果被删除的结点是根结点,又可分以下两种情况。
被删除结点无左子树,则以被删除结点的右子树作为删除后的二叉排序树;
被删除结点有左子树,则用被删除结点的左子结点作为根结点,并把被删除结点的右子树作为被删除结点的左子树按中序遍历的最后一个结点的右子树。
②如果被删除结点不是根结点,且被删除结点无左子结点,则,
被删除结点是它父结点的左子结点,则把被删除结点的右子树作为被删除结点父结点的左子树;
被删除结点是它父结点的右子结点,则把被删除结点的右子树作为被删除结点父结点的右子树;
③如果被删除结点不是根结点,且被删除结点无左子结点,则被删除结点的右子树作为被删除结点的左子树按中序遍历的最后一个结点的右子树,同时进行以下操作:
被删除结点是它父结点的左子结点,则把被删除结点的左子树作为被删除结点父结点的左子树;
被删除结点是它父结点的右子结点,则把被删除结点的左子树作为被删除结点父结点的右子树。








