信息系统运行管理员基础知识：数制转换

1. 十进制转R进制

1.1. 十进制转二进制

(1)十进制整数转二进制

十进制整数转换成二进制采用“除2倒取余法”，即将十进制整数除以2.得到一个商和一个余数;再将商除以2.又得到一个商和一个余数;以此类推，直到商等于零为止。

例题： 175D = ___ B

解析：如下图所示，将175除以2.得余数，直到不能整除，然后再将余数从下至上倒取。得到结果：10101111B。

135D = ______ B

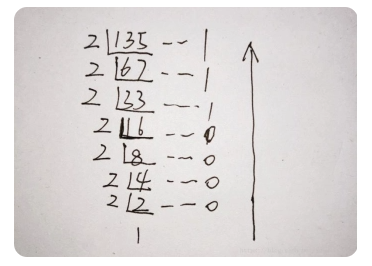
135D = 1000 0111B

(2)十进制小数转二进制

十进制小数转换成二进制小数采用 “乘2取整，顺序排列”法。

具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数 部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。

然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。例题： 0.68D = ___ B(精确到小数点后5位)

解析：如下图所示，0.68乘以2.取整，然后再将小数乘以2.取整，直到达到题目要求精度。得到结果：0.10101B

1.2. 十进制转八进制

思路和十进制转二进制一样，参考如下例题：

例题： 10.68D = ___ Q(精确到小数点后3位)

解析：如下图所示，整数部分除以8取余数，直到无法整除。小数部分0.68乘以8.取整，然后再将小数乘以8.取整，直到达到题目要求精度。得到结果：12.534Q

1.3. 十进制转十六进制

思路和十进制转二进制一样，参考如下例题：

例题： 25.68D = ______ H(精确到小数点后3位)

解析：如下图所示，整数部分除以16取余数，直到无法整除。小数部分0.68乘以16.取整，然后再将小数乘以16.取整，直到达到题目要求精度。得到结果：19.ae1H

2. R进制转十进制

2.1. 二进制转十进制

方法为：把二进制数按权展开、相加即得十进制数。(具体用法如下图)

例题： 1011 0111B = ______ D

解析：10110111B=1×2^7+0×2^6+1×2^5+1×2^4+0×2^3+1×2^2+1×2^1+1×2^0=128+0+32+16+0+4+2+1=183

2.2. 八进制转十进制

八进制转十进制的方法和二进制转十进制一样。

例题： 302Q = ___ D

302.46Q = ___ D

解析：302Q = 3×8^2+ 0×8^1 + 2×8^0= 192 + 0 + 2 = 194D

302.46Q = 3×8^2 + 0×8^1+ 2×8^0+ 4×8^-1 + 6×8^-2= 192 + 0 + 2 + 0.5 + 0.09375= 194.59375D

2.3. 十六进制转十进制

例题： 23daH = ______ D

解析：23daH = 2×16^3+3×16^2+d×16^1+a×16^0= 9178D

3. 二进制转八进制

二进制转换成八进制的方法是，取三合一法，即从二进制的小数点为分界点，向左(或向右)每三位取成一位。

例题： 1010 0100B = ____Q

解析：1010 0100B = 010 001 100 B=244Q

4. 二进制转十六进制

二进制转换成八进制的方法是，取四合一法，即从二进制的小数点为分界点，向左(或向右)每四位取成一位。

例题： 1010 0100B = ____H

解析：1010 0100B = 1010 0100 B = a4H

综合上述所介绍的，我们可以知道的是二进制转八进制或者二进制转换成十六进制，也可以先转换成十进制，再转换成目标进制。